Số hữu tỉ là gì?

Công thức số hữu tỉ và số vô tỉ là những kiến thức quan trọng trong toán học mà các bạn học sinh phải nắm rõ để có được nền tảng toán học vững chắc. Bài viết này sẽ giới thiệu đến bạn định nghĩa, tính chất, các dạng toán của số hữu tỉ, số vô tỉ, mời các bạn tham khảo.

1. Số hữu tỉ là gì?

- Số hữu tỉ là tập hợp các số có thể viết được dưới dạng phân số (thương số). Tức là một số hữu tỉ có thể được biểu diễn bằng một số thập phân vô hạn tuần hoàn.

- Số hữu tỉ được viết là $\frac{a}{b}$ , trong đó a và b là các số nguyên nhưng b phải khác 0.

- $\mathbb{Q}$ là tập hợp các số hữu tỉ.

=> Tập hợp số hữu tỉ: $\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z},b \ne 0} \right\}$ .

Ví dụ: $-3; -1,75$ , $4\frac{1}{5}$ , … là các số hữu tỉ.

Số nguyên a bất kì là một số hữu tỉ vì số nguyên a có thể viết dưới dạng $\frac{a}{1}$ .

Ví dụ: Ta có $1; -3; 0$ là các số hữu tỉ.

Ta có:

$\begin{matrix}1 = \dfrac{1}{1} \Rightarrow 1\mathbb{\in Q} \\- 3 = \dfrac{- 3}{1} \Rightarrow - 3\mathbb{\in Q} \\0 = \dfrac{0}{1} \Rightarrow 0\mathbb{\in Q} \\\end{matrix}$

Nhận xét: $\mathbb{Z =}\left\{ 0; \pm 1; \pm 2;... \right\}$ đều là số hữu tỉ.

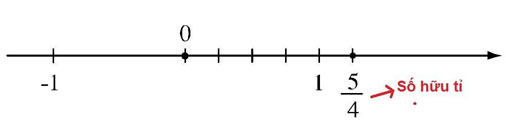
Số hữu tỉ

Phân loại số hữu tỉ

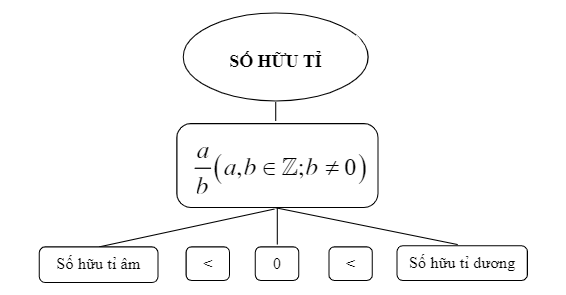
Số hữu tỉ được phân thành 2 loại gồm số hữu tỉ âm và số hữu tỉ dương. Cụ thể:

Số hữu tỉ âm: Bao gồm những số hữu tỉ nhỏ hơn 0.
Số hữu tỉ dương: Bao gồm những sổ hữu tỉ lớn hơn 0.

Lưu ý: Số 0 không phải là số hữu tỉ âm và cũng không phải là số hữu tỉ dương.

Số hữu tỉ

Tính chất

Tập hợp số hữu tỉ là tập hợp đếm được.
Tính chất giao hoán: $x + y = y + x$
Tính chất cộng với 0: $x + 0 = y + 0$
Tính chất kết hợp: $(x + y) + z = x + (y + z)$

Biểu diễn số hữu tỉ trên trục số

- Để biểu diễn số hữu tỉ trên trục số ta làm theo các ước sau:

Bước 1: Viết số hữu tỉ dưới dạng phân số $\frac{a}{b}$

Bước 2: Chia đoạn thẳng đơn vị thành b phần bằng nhau ta được đoạn đơn vị mới là $\frac{1}{b}$ đơn vị cũ.

Bước 3: Số hữu tỉ $\frac{a}{b}$ được biểu diễn bằng điểm A cách điểm 0 một đoạn bằng a đơn vị mới.

A nằm bên trái điểm 0 nếu là số âm.
A nằm bên phải điểm 0 nếu là số dương.

Ví dụ: Trên hình vẽ, điểm P biểu diễn số hữu tỉ là:

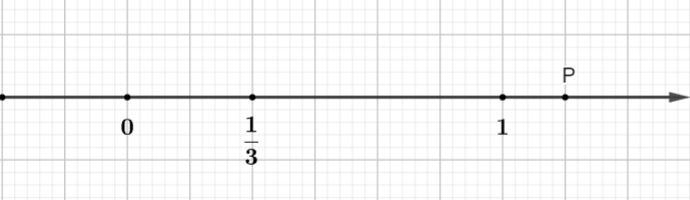
Số hữu tỉ

Hướng dẫn

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau (đơn vị mới bằng 1/6 đơn vị cũ)

Điểm P nằm ở vị trí cách điểm O một đoạn bằng 7 đơn vị mới

Và điểm P nằm bên phải điểm O nên P là một số hữu tỉ dương

Vậy P biểu diễn số hữu tỉ $\frac{7}{6}$ .

Cộng, trừ số hữu tỉ

i) Quy tắc cộng, trừ hai số hữu tỉ

Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số rồi áp dụng quy tắc cộng, trừ phân số

Với $x = \frac{p}{m};y = \frac{q}{m};\left( p,q,m\mathbb{\in Z},m > 0 \right)$ ta có:

$x + y = \frac{p}{m} + \frac{q}{m} = \frac{p + q}{m}$

$x - y = \frac{p}{m} - \frac{q}{m} = \frac{p - q}{m}$

ii) Tính chất

- Phép cộng số hữu tỉ có tính chất của phép cộng phân số: Giao hoán, kết hợp, cộng với 0, cộng với số đối.

- Với $a,b,c\mathbb{\in Q}$ ta có:

a) Tính chất giao hoán: $a + b = b + a$

b) Tính chất kết hợp: $a + (b + c) = (a + b) + c$

c) Cộng với số 0: $a + 0 = 0 + a = a$

d) Cộng với số đối: $a + (-a) = 0$

iii, Quy tắc chuyển vế

Khi chuyển vế một số hạng tử từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Trong Q ta có tổng đại số, trong đó có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng đại số trong tập số nguyên

Với $a,b,c\mathbb{\in Q}$ nếu $a + b = c$ thì $a = -b + c$
Với ta có:
- $x - (y - z) = x - y + z = x + z - y$
- $x - y + z = x - (y - z)$

Nhân, chia số hữu tỉ

i) Quy tắc nhân, chia hai số hữu tỉ

- Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Với $x = \frac{a}{b};y = \frac{c}{d};(b,d \neq 0)$ ta có: $xy = \frac{a}{b}.\frac{c}{d} = \frac{ac}{bd}$
Với $y \neq 0$ ta có: $x:y = \frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{ad}{bc}$

Ví dụ:

Nhân số hữu tỉ: $\frac{2}{5}\times\frac{7}{3}\times\frac{2}{3}=\frac{28}{45}$

Chia số hữu tỉ: $\frac{4}{5}\div\frac{3}{7}=\frac{4\times7}{5\times3}=\frac{28}{15}$

ii) Tính chất

- Phép nhân số hữu tỉ cũng có các tính chất như phép nhân phân số: Giao hoán, kết hợp, nhân với 1 và tính chất phân phối của phép nhân đối với phép cộng.

- Mọi số hữu tỉ khác 0 đều có một số nghịch đảo.

- Với $a,b,c\mathbb{\in Q}$ ta có:

Tính chất giao hoán: $a.b = b.a$ .
Tính chất kết hợp: $a.(b.c) = (a.b).c$ .
Tính chất nhân với 1: $a.a = 1.a = a$ .
Tính chất phân phối: $a.(b + c) = a.b + a.c$ .
Với $a\mathbb{\in Q},a \neq 0$ . Số nghịch đảo của a là $\frac{1}{a}$ .

Giá trị tuyệt đối của một số hữu tỉ

- Giá trị tuyệt đối của một số hữu tỉ a, kí hiệu là $|a|$ , là khoảng cách từ điểm a đến điểm 0 trên trục số.

$|a| = \left\{ \begin{matrix} a\ \ \ \ \ \ \ khi\ \ a \geq 0\ \ \\ - a\ \ \ \ khi\ \ a < 0 \\ \end{matrix} \right.$

Ví dụ:

$x = \frac{1}{5} \Rightarrow |x| = \left| \frac{1}{5} \right| = \frac{1}{5}$ (Vì $\frac{1}{5} > 0$ )

$x = - 1\frac{3}{4} \Rightarrow |x| = \left| - 1\frac{3}{4} \right| = - \left( - 1\frac{3}{4} \right) = 1\frac{3}{4}$ (Vì $- 1\frac{3}{4} < 0$ )

So sánh hai số hữu tỉ

- Với 2 số hữu tỉ bất kì $x, y$ ta luôn có hoặc $x = y$ hoặc $x < y$ hoặc $x > y$ .

- Để so sánh hai số hữu tỉ $x, y$ ta làm như sau:

Viết $x, y$ dưới dạng 2 phân số cùng mẫu dương: $x = \frac{a}{m};y = \frac{b}{m};(m >0)$
So sánh tử số là các số nguyên a, b:

$\begin{matrix} a < b \Rightarrow x < y \\ a > b \Rightarrow x > y \\ a = b \Rightarrow x = y \\ \end{matrix}$

Ví dụ: So sánh hai số hữu tỉ: $\frac{- 2}{5}$ và $\frac{3}{- 4}$

Ta có: $\frac{- 2}{5} = \frac{- 2.4}{5.4} = \frac{- 8}{20}$

$\frac{3}{- 4} = \frac{3.( - 5)}{( - 4).( - 5)} = \frac{- 15}{20}$

Vì $-8 > -15, 20 > 0$ nên $\frac{- 8}{20} > \frac{- 15}{20}$ hay $\frac{- 2}{5} > \frac{3}{- 4}$ .

Công thức tính lũy thừa của một số hữu tỉ

Các công thức tính lũy thừa của 1 số hữu tỉ mà bạn cần phải ghi nhớ

Tích của hai lũy thừa cùng cơ số: $X^m.X^n=X^{m+n}$
Lũy thừa của lũy thừa $\left(X^m\right)^n=X^{m.n}$
Lũy thừa của một tích $\left(X.Y\right)^n=X^n.Y^n$
Lũy thừa của một thương $\left(\frac{X}{Y}\right)^n=\frac{X^n}{Y^n}$

2. Số vô tỉ là gì?

Khái niệm số vô tỉ

Nhắc tới số hữu tỉ người ta không thể không nhắc đến số vô tỉ, đây là các số được viết ở dạng thập phân vô hạn không tuần hoàn, kí hiệu là $\mathbb{I}$ .
Các số thực không phải là số hữu tỉ thì không thể biểu diễn dưới dạng tỉ số.

Ví dụ: 3,145248… là số vô tỉ.

Tính chất của số vô tỉ

Tập hợp số vô tỉ là tập hợp không đếm được.

Ví dụ:

Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn không tuần hoàn)

Số căn bậc 2: √2 (căn 2)

Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Số vô tỉ

3. Sự khác nhau giữa số hữu tỉ và số vô tỉ?

Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn, còn số vô tỉ là các số thập phân vô hạn không tuần hoàn.
Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số khác nhau
Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được

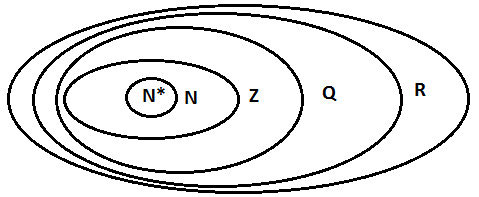
4. Mối quan hệ các tập hợp số

Ký hiệu các tập hợp số:

N: Tập hợp số tự nhiên
N*: Tập hợp số tự nhiên khác 0
Z: Tập hợp số nguyên
Q: Tập hợp số hữu tỉ
I: Tập hợp số vô tỉ

Ta có: R = Q ∪ I.

Tập N ; Z ; Q ; R.

Khi đó quan hệ bao hàm giữa các tập hợp số là : N ⊂ Z ⊂ Q ⊂ R

Mối quan hệ các tập hợp số

5. Các dạng bài tập về số hữu tỉ

Dạng 1: Thực hiện các phép tính có liên quan đến số hữu tỉ

Phương pháp giải: Để giải các bài tập về thực hiện phép tính có liên quan đến số hữu tỉ, đầu tiên cần đưa các số hữu tỉ về dạng phân số, sau đó áp dụng các quy tắc tính toán với phép tính cộng, trừ, nhân, chia số hữu tỉ.

Ví dụ: Tính $-\frac{5}{3}\div\frac{7}{4}$

Đáp án: $-\frac{5}{3}\div\frac{7}{4}=-\frac{5}{3}\times\frac{4}{7}=-\frac{5\times4}{3\times7}=-\frac{20}{21}$

Dạng 2: Biểu diễn số hữu tỉ trên trục số

Phương pháp giải: Cần xác định số hữu tỉ là số hữu tỉ dương hay số hữu tỉ âm, sau đó tiếp tục thực hiện các bước tiếp theo:

Nếu số hữu tỉ a/b là số hữu tỉ dương: Trên trục số, chiều dương trục, tiến hành chia độ dài 1 đơn vị thành b phần bằng nhau. Sau đó lấy điểm trên chiều dương trục Ox điểm a phần và xác định vị trí số hữu tỉ a/b.
Nếu số hữu tỉ a/b là số hữu tỉ âm: Trên trục số, chiều âm trục, tiến hành chia độ dài 1 đơn vị thành b phần bằng nhau. Sau đó lấy điểm trên chiều âm trục Ox điểm a phần và xác định vị trí số hữu tỉ a/b.

Dạng 3: So sánh số hữu tỉ

Phương pháp giải: Đưa các số hữu tỉ đã cho về dạng phân số có cùng mẫu số dương, sau đó tiến hành so sánh tử số. Nâng cao hơn chúng ta có thể thực hiện việc so sánh với phân số trung gian để tìm ra đáp án.

Dạng 4: Xác định số hữu tỉ là âm, dương hay 0

Phương pháp giải: Giải bài tập dạng 4 học sinh cần căn cứ vào tính chất của số hữu tỉ để xác định số hữu tỉ là số âm, số dương hay là 0.

Ví dụ: Cho số hữu tỉ x = (a – 25)/29, hãy xác định giá trị của a để:

x là số âm
x là số dương
x = 0

Đáp án:

x là số âm => (a – 25)/29 < 0 => a – 25 < 0 => a < 25

x là số dương => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Dạng 5: Tìm số hữu tỉ trong khoảng theo điều kiện cho trước

Phương pháp giải: Nếu đề bài yêu cầu tìm số hữu tỉ theo trong khoảng theo điều kiện cho trước, chúng ta cần đưa các số hữu tỉ về cùng tử số hoặc mẫu số để tìm ra đáp án.

Ví dụ: Tìm giá trị của m để $\frac{m}{18}$ lớn hơn $\frac{- 5}{6}$ và nhỏ hơn $\frac{- 1}{2}$

Hướng dẫn đáp án

Quy đồng mẫu số các phân số như sau:

Mẫu thức chung: 18

$\begin{matrix}\dfrac{- 5}{6} = \dfrac{- 5.3}{6.3} = \dfrac{- 15}{18} \\\dfrac{- 1}{2} = \dfrac{- 1.9}{2.9} = \dfrac{- 9}{18} \\\end{matrix}$

Theo đề bài ra ta có:

$\begin{matrix} \dfrac{{ - 5}}{6} < \dfrac{m}{{18}} < \dfrac{{ - 1}}{{12}} \hfill \\ \Rightarrow \dfrac{{ - 15}}{{18}} < \dfrac{m}{{18}} < \dfrac{{ - 9}}{{18}} \hfill \\ \Rightarrow - 15 < m < - 9 \hfill \\ = > m \in \left\{ { - 14; - 13; - 12; - 11; - 10} \right\} \hfill \\ \end{matrix}$

Dạng 6: Tìm x với số hữu tỉ

Phương pháp giải dạng toán: Với dạng toán tìm x với số hữu tỉ cần phải thực hiện quy đồng khử mẫu số và chuyển x về 1 vế, các số hạng còn lại về 1 về. Từ đó tính giá trị của x

Ví dụ: Tìm x biết x . (2/ 3) + 5/ 6 = 1/ 8

Đáp án:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Dạng 7: Tìm a để biểu thức là số nguyên

Phương pháp giải dạng toán: Đối với bài toán tìm a nếu tử số không chứa a chúng ta cần sử dụng dấu chia hết, nếu tử số chứa a dùng dấu chia hết hoặc tách tử số theo mẫu số. Nếu bài toán yêu cầu tìm đồng thời cả a, b cần nhóm a hoặc b và đưa về dạng phân thức để tính.

Ví dụ: Tìm số nguyên a với điều kiện 8/(a – 1) là số nguyên

Đáp án:

Điều kiện: a – 1 ≠ 0 => a ≠ 1

Để a là số nguyên => 8 chia hết cho (a – 1)

=> (a – 1) là ước của 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Hi vọng với nội dung bài viết trên đã giúp bạn nắm được số hữu tỉ là gì, số vô tỉ là gì, các loại số hữu tỉ, số hữu tỉ kí hiệu là gì, cách nhận biết số hữu tỉ để giải quyết các bài toán dễ dàng nhé. Ngoài các kiến thức về số vô tỉ, số hữu tỉ trên, các bạn có thể tham khảo thêm một số kiến thức toán học khác như phân số, hỗn số, số thập phân...